8.01. Families of cosmological principles
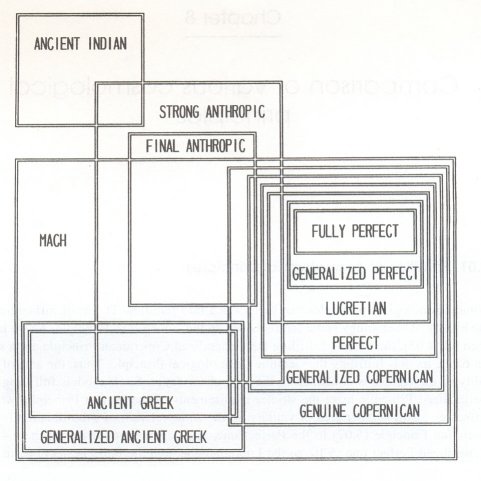
Some cosmological principles can be grouped into families. The most influential in the history of cosmology is the family based on the Copernican Principle. As we have seen (cf. 4.03), the models fulfilling the Generalized Copernican Principle are a subset of the models fulfilling the Genuine Cosmological Principle. Thus, the area of validity of the former is contained in the area of the latter. Some models fulfilling the Generalized Principle meet the stricter requirements of the Perfect Principle, which possesses a still smaller area of validity. In the same relation of subordination is the Lucretian Principle (5.07) to the Perfect one, and - if one would accept them - the Generalized Perfect one (5.10) to the Lucretian one, and the Fully Perfect one to the Generalized Perfect one. Of course, the entire family falls into the area of validity of Mach's Principle (6.06). Here we can also add the Homogeneity Principle, which is situated between the Genuine and the Generalized Copernican principles.
Analogously, the area of Mach's Principle includes the Generalized Ancient Greek Principle and, as a part of the last one, the Ancient Greek Principle (here the generalization makes the requirements less strict, cf.: 2.13).
The Ancient Indian Principle remains beyond the scope of Mach's principle. It leaves no possibility of extrapolation and forms a separate area of validity.
The Strong Anthropic Principle can be reconciled with Mach's as well as with the Ancient Indian principles. The Final Anthropic Principle, however, contradicts the Ancient Indian one.
Mutual relations of the above mentioned principles are presented in the following figure:
8.02. Infinity of the Universe. Space symmetries
First I would like to compare some of specifications of the six main principles described in Chapters 1 through 6. The first is the possibility of considering the Universe as spatially finite or infinite. Some of principles involve, in an explicit or implicit way, the conviction that the dimensions of the Universe are infinite (Ancient Indian and Perfect principles). Others allow for conceiving the Universe as finite as well. Two historical principles (the Ancient Greek and the Genuine Copernican) do not touch upon this issue. We could study the views of the Ancients on the infinity of space, but they are of no concern for cosmological principles. Of course, one can state that Aristotle considered the Universe to be finite and provided some philosophical arguments to support that statement. However, the opinion that his model of the Universe was finite is not implied by the accepter cosmological principle. Analogously, one may ask whether, for example, the Empyrean was imagined as finite or not, but this will be a question concerning some feature of a certain model, not the Cosmological Principle of Ancient Greeks as such. These two historical principles, when submitted to logical analysis, yield no requirements about the size of the Universe. So we have to consider them as allowing both finite and infinite size. It is remarkable that there are cosmological principles permitting finite dimensions of the Universe and those permitting infinite ones. There are cosmological principles requiring the infinity of the Universe (the Ancient Indian and the Perfect ones), but none is known which would require its finiteness. Does this mean that the human mind is always more inclined to see the Universe as infinite rather than finite?
No strict space symmetry is demanded by the Ancient Indian Principle, but the Universe is regarded as spatially infinite in all directions. For the Anthropic Principle, when considered independently from the Copernican Principle (without assuming Hubble's Law), the problem of symmetry in various space directions is irrelevant. This principle can allow the existence of torus-like spaces with some dimensions finite and some infinite. It is worthwhile to note that assumptions equivalent to cosmological principles, which are used in discussing Kaluza-Klein type universes, usually require either that the Universe be infinite in three dimensions (the "ordinary" spatial dimensions accessible to our senses) and finite in the seven others, or, more often, that it be finite in all 10 spatial dimensions. The three "ordinary" dimensions differ from the other seven only in space curvature. However, this does not belong to any of the six main cosmological principles.
8.03. Origin and end of the Universe
Another fundamental specification relates to the beginning and the end of the Universe, or, in other words, the issue of its finite and infinite duration in time. Again, we find some similarities. There are principles requiring infinity in time (the Ancient Indian and the Perfect) but none requiring finiteness. This is the case even in the Generalized Copernican Principle. It produces Hubble's Law, but Hubble's constant can be, in theory, equal to zero. The Big Bang theory is not a necessary implication of this principle but just one (certainly the most remarkable!) of the possibilities. Thus even this principle, which undoubtedly favors most the finite duration of the Universe, does not necessarily require it.
All that can be said about the age of the Universe on the basis of the Strong Anthropic Principle can be deduced only by accepting the Copernican Principle. The Strong Anthropic Principle as such states nothing about the beginning or the end of the Universe. The Final Anthropic Principle, when considered as a cosmological principle, demands that there has been a beginning of the Universe (cf. 6.20).
Time can be finite in one direction but infinite in another. No principle which allows finite time demands any symmetry.
8.04. Center of the Universe
The third important specification of cosmological principles is the existence of any center of the Universe. Only the Genuine Copernican and the Anthropic principles are liberal enough to allow both existence and non-existence of some central body or central point of the Cosmos. All the other ones do not allow any center, except for the Ancient Greek Principle which does demand a center and is thus in extreme opposition to them.
These most important specifications can be presented in the form of a table which can also include some less popular cosmological principles.
| Designation of | Spatial infinity | Existence of | time of | Existence of a |
| the principle | beginning | end | spatial center | |
| Ancient Indian | I | O | O | O |
| Ancient Greek | = | = | = | I |
| Generalized Ancient Greek | = | = | = | I |
| Genuine Copernican | = | = | = | = |
| Softened Copernican | = | = | = | ? |
| Generalized Copernican | = | = | = | O |
| Perfect | I | O | O | O |
| Lucretian | I | O | O | O |
| Generalized Perfect | I | O | O | O |
| Fully Perfect | I | O | O | O |
| Strong Anthropic | = | = | = | = |
| Final Anthropic | I | I | = | = |
| Fractal | I | = | = | O |
| Weyl's postulate | = | O | O | ? |
