We now come to that part of twentieth century physics which involves the unpredictable, as well as a major rethinking about the nature of space and time. This physics sprang from the study of various phenomena, mainly the interaction of light with matter, what happens when electricity crosses a near vacuum, radioactivity and, in general, from studies of what occurs over very short distances on very small sub-microscopic scales, as well as what occurs when very small differences of energy are involved. The small distances and small differences of energy cannot be directly perceived by a human being, but only by the measuring instruments. One possible definition of what such small distance scales are at which phenomena occur and which appear strange compared with what humans normally perceive, was once given by R. Burlotte at a meeting in Chatou near Paris. He considered this to be the scale at which the chemical properties of substances no longer existed, that is, scales smaller than that of the molecules from which chemical compounds are made. Let us recall that, as mentioned in chapter two, a molecule of a compound is defined as consisting of a number of atoms. Other definitions of these small scales are, however, possible. For instance, bodies which exist at these scales can keep an electric charge indefinitely, unlike in the everyday world where bodies with a positive electric charge tend to meet bodies carrying a negative charge after a relatively short time. The final result in the everyday world is that both the negative and positive charges are cancelled.

We have already discussed spectrums in chapter two. Now, in order to understand the quantum world discussed in this section, we must look more closely at what kinds of spectrums exist. A very important discovery of nineteenth century physics was that different substances do not emit and absorb light in the same way. Gasses, when heated or made to emit radiation by another process in the laboratory, will usually only emit light having certain colours when the radiation is visible to the human eye. In general, if we describe what happens in the framework of the theory of electromagnetic waves, not only considering visible light but also other sorts of radiation, most radiation emitted will have certain well defined wavelengths. Substances which emit at a given wavelength will also absorb radiation coming from the outside at the same wavelength. Dense substances, unlike gasses, will emit almost all their radiation over a very wide range of wavelengths. Instruments containing prisms or what are called "gratings", which act similarly to prisms, can be constructed in order to examine the spectrum of each substance. By using such instruments astronomers are able to detect the presence of chemical elements in stars and make deductions about the physical conditions of the layers of the star from which the emitted light comes. This is possible because different elements having different conditions will not emit and absorb light in the same way, so the spectra will not be the same. Most of my official scientific work in astrophysics is concerned with the study and interpretation of the spectra of certain rather special types of stars.

The first form of what was to become "quantum theory" originated in 1900 from work of the German physicist Max Planck on the amount of electromagnetic radiation emitted at different wavelengths by a body which is also able to absorb all such radiation falling on it, that is, radiation emitted by what physicists call a "black body". Such a body emits its radiation over a very wide range of wavelengths. Planck found that it was necessary to suppose that this radiation was emitted in separate packets, each containing a finite amount of energy. A packet or "quantum" of radiation emitted at a shorter wavelength than another packet, will contain more energy than that emitted at a larger wavelength. This energy is mathematically expressed as being equal to hc/l, where h is a basic physical constant called Planck's constant, c is the speed of light and l is the wavelength the radiation would have if it were crossing a "vacuum", that is, a region containing no matter. Planck's constant is very small, so the separate packets are not seen at the human scale, at which radiation appears to be continuous.

Another phenomenon, discovered by Einstein in 1905, indicates that electromagnetic radiation behaves in certain situations as if it were made of particles. When what is called the "photoelectric effect" occurs, light falling on certain metals will produce electricity. Whether or not electricity is produced does not depend on the intensity of the light, but only on the energy which is contained in each quantum of light falling on the metal. For less than a certain amount of energy no electricity is produced.

In fact, the electricity produced by the photoelectric effect appeared to be carried by particles with a negative electrical charge, called "electrons", the existence of which had been previously indicated by experimental studies at the end of the nineteenth century. These experiments involved the passage of electricity in tubes from which all or almost all gases had been removed. It was by using such methods that certain properties of a single electron were determined by J.J. Thomson in 1897. The electrons seemed to have been separated from atoms which, having lost negatively charged electrons, acquired a positive electric charge.

It was with the help of such ideas that the photoelectric effect was understandable: if light could behave as if it consisted of particles which, when they had more than a certain amount of energy before striking the surface of a metal, caused the ejection of other particles, that is, of electrons.

Another phenomenon was discovered by H. Becquerel in 1896. He found that compounds of the element uranium emitted something which could affect photographic plates, even when the photographic plate was separated from the uranium by black paper. Other elements were then discovered to have this property of "radioactivity". It was then found that what was emitted by radioactive elements included electrons moving at very high speeds, electromagnetic radiation having very short wavelengths, (that is, possessing quanta with very high energy) as well as atoms of the element helium with a positive charge. In this way the rules of nineteenth century chemistry were violated by radioactivity. Atoms of a radioactive element produced high velocity atoms of another element, helium, while they themselves were transformed into atoms of a third element. The energy per atom involved in these and other radioactive transformations was, however, much higher than in those of chemistry, in which different atoms combined to form molecules.

The question then arose as to what was the structure of an atom. It seemed to contain electrons and something possessing a positive electrical charge, so that a normal atom is electrically neutral. J.J. Thomson thought that the electrons of an atom were surrounded by the positive charge. This concept was disproved by Rutherford, using the helium atoms with a positive electrical charge emitted by radioactive substances. Two electrically charged bodies having the same charge repel each other, so the positively charged helium atoms coming close to other atoms should be repelled. Rutherford showed that only a small proportion were repelled, some being repelled very strongly. He explained this as being due to the fact that the positive charge of an atom was concentrated in a nucleus, which was much smaller than an atom. The nucleus moreover contained almost all the mass of the atom. It is in the framework of Rutherford's model that the atom and therefore matter began to appear as being almost empty; that is, matter began to appear as something not quite material! Radioactivity came to be understood as due to changes in the nucleus, which was transformed from that of one element into that of another, by emitting positively charged helium atoms, or by emitting electrons, or by sometimes changing in another way.

The nucleus, which could be transformed if it were radioactive or if it were struck by what appeared to be a particle, was considered to contain several particles. One type of particle in the nucleus having a positive electric charge was called a proton, while the other type, which was electrically neutral, was called a neutron. It was first thought that there were electrons in the nucleus, but this idea was abandoned following the discovery of the neutron. As there were only positively charged particles (which, having the same electric charge, should repel each other) and electrically neutral particles in the nucleus, a new strong "nuclear" force was needed to hold the particles in the nucleus together.

Once a "picture" of the structure of an atom had been established, it was possible to study its physics and to further elaborate the quantum theory. According to this picture the electrons of an atom revolved around the much more massive nucleus in the same way that the planets revolve around the Sun. In the case of the atom the forces were electrical, while those attracting a planet to the Sun were gravitational. However, according to classical theory, a negative charge revolving around a positive charge should emit electromagnetic radiation and fall towards the positive charge. An atom with this type of structure should then not be stable. A major step to overcome this problem and also to explain the spectrum emitted by the chemical element hydrogen was taken by Niels Bohr in 1913. Electrons were only able to revolve in well defined orbits around the nucleus. Quanta of electromagnetic radiation were sometimes emitted when electrons jumped from one orbit to another. According to this conception electrons could either spontaneously jump or be made to jump. It was possible to explain many things and not only certain properties of spectra by this "old quantum theory". However, its basis was inconsistent, containing both classical physics and quantum theory. Moreover, it could not explain all spectra. Although the idea of an atom being like a small solar system was soon found to be wrong, it has remained in the popular imagination. It is a very good example of how the thinking of people can be influenced and perhaps even manipulated by a scientific idea which is out of date!

More radical changes in the basis of physics were needed. A most important step was taken by De Broglie in 1923 when he showed that not only did electromagnetic radiation behave as though it were composed of particles, but also that the particles of which matter appeared to be made also had wavelike properties. The wavelength of such a particle equals h/(mv), where h is Planck's constant, m is the mass which must be corrected at high velocities for the increase in its value predicted by special relativity, and v the velocity of the particle (the multiple of m and v is equal to what is called "momentum" in classical physics). This theoretical prediction was experimentally confirmed; these particles could really behave as waves. The mathematical work of Erwin Schrödinger established what is called "wave mechanics", which was able to explain the validity of the previously apparently arbitrary assumptions of the old quantum theory. An atom can only have certain well defined stable wave structures which endure in the framework of this theory and which correspond to the idea of the existence of arbitrary stable orbits in Bohr's theory. Thus an extremely surprising, apparently paradoxical situation had arisen, with two contradictory pictures being needed; one described the world in terms of particles, while the other described the world in terms of waves. The possible meaning of such a result and further developments will be examined in the next two sections.

The paradoxical nature of quantum physics becomes clear when we consider what happens during certain experiments performed to test the various ideas of this physics. Different, apparently contradictory conclusions about what has happened in the laboratory will be obtained, depending on which experiment is performed. For example, certain experiments will show the presence of waves while others will show the presence of particles. It is as if Nature resists the experimenter and gives contradictory answers, depending on which question is asked!

In order to understand the nature of waves in physics, let's look at a very simple situation, shown in fig.3.4. Circular waves on the surface of a lake coming from a disturbance at a point in the lake can only pass through two holes in a barrier. They then reach a side of the lake. At certain points on that side the effects of the waves which have come through each of the holes on the surface of the lake will increase; when waves which have come through one hole tend to raise the surface of the lake, waves which have come through the other hole will also have the same effect. At other times, when waves which have come through one of the holes tend to lower the surface of the water at such a point, waves which have come through the other hole will also tend to lower the surface. Therefore the effects of the waves coming through both holes will reinforce each other at these points on the side of the lake. At other points on the side of the lake the effect of waves which have come through one hole will cancel the effect of those which have come through the other; when waves from one hole tend to raise the surface of the lake, waves from the other hole tend to lower it. At such points the waves may have no effect on the surface of the lake, which then does not move. This is the situation when what is called "interference" occurs, that is, interference between the waves coming through each of the two holes. This can be shown to happen for light and also for the "particles" of modern physics, when the holes are very small. If they only behaved as one expects particles to behave, the situation would be quite different. Let us suppose that small pieces of wood floating on the surface of the lake, which behave like particles, also go through both holes; the number of pieces of wood arriving at any point on the side of the lake will then be the sum of the numbers of those which have gone through each hole. Therefore, waves cannot be particles and particles cannot be waves in classical physics.

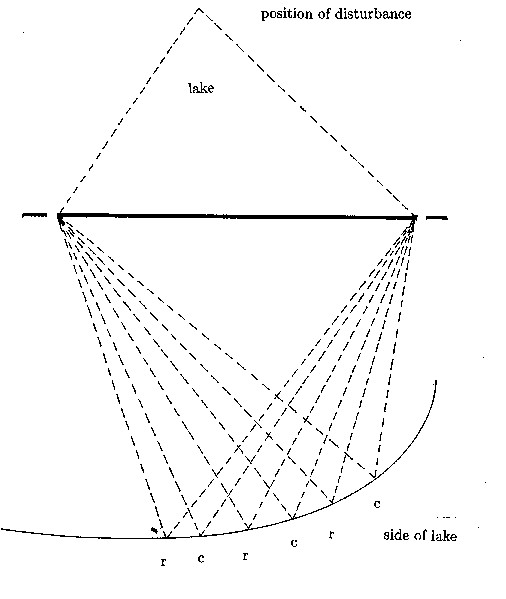
Fig. 3.4 - Waves due to a disturbance at a position in a lake which interfere after passing through 2 holes of an obstacle. At the points labeled r on the side of the lake the waves reinforce each other; at points labeled c they cancel each other out. The dashed lines indicate the paths taken by the waves to each point on the side of the lake.

Another characteristic of waves is that a wave of arbitrary shape can be considered to be a sum of regular sine waves, having different wavelengths (for each sine wave there is a property, which at a certain time varies with position in the same way that the sine function of elementary trigonometry varies with angle). In this way, by adding waves with extremely different wavelengths, it is possible to have what is called a "wave packet", which is very strong in one place and weak elsewhere, behaving in some ways like a particle. Adding waves of very similar wavelengths will on the other hand produce a sum which is very extended in space. It might be thought that one could explain the observed phenomena without assuming the presence of particles, by supposing that only sums of waves with different wavelengths are present. This does not work however, as the wave packets would increase in size with time, while experiments show that particle-like behavior can still occur.

As we have seen, quantum physics appears to contradict classical physics. There are objects which can behave both as particles and waves. This contradiction was overcome by Max Born's idea that the waves are not simply waves occuring in matter like those of the surface of the lake, but waves related to the probability of finding a particle with a certain velocity at a certain point at a certain time. This probability can be calculated from what is called the "amplitude" of the wave. In respect to the waves on the lake just mentioned, this amplitude would be the height of those waves. However, it is impossible to know exactly where a particle will be at a certain time or exactly what its velocity will be.

This interpretation in terms of probability can be understood if we consider a fundamental discovery by W. Heisenberg, which will be extremely important for what is discussed later in this book. This is the so-called "indeterminacy" or "uncertainty principle". According to this principle, it is impossible to measure (and, according to the interpretation accepted by most physicists, even to define) with more than a certain accuracy both the position and speed of a moving particle at a certain time. If the uncertainty in the determination of the position x is Dx and the uncertainty in the determination of mass m times velocity v is Dmv, one finds that

Dt times Dmv�h/(2p)

In this mathematical expression � means greater than or equal to; the Heiseneberg indeterminacy principle states that the left-hand side of the expression can never be less than the right-hand-side. This condition can also be stated in terms of time and energy. If an event requiring an energy E occurs at a time t and Dt is the uncertainty in the determination of t, while DE is the corresponding uncertainty in the determination of E:

Dt times DE � h/(2p)

In the case of a moving particle with a velocity v, Dt is in the second form of the Heisenberg indeterminacy principle, the time needed for it to cross the distance Dx, while DE is the uncertainty in the determination of the amount of energy contained in its movement (kinetic energy). The second form of the Heisenberg uncertainty principle is also true when an atom emits a quantum of radiation; if the quantum can be emitted at a time within a time interval of D t, it is impossible to specify exactly what its energy is to an accuracy of more than the value of DE.

The resistance to an experimenter by nature mentioned at the beginning of this section can be stated in terms of the Heisenberg uncertainty principle. Nature resists the simultaneous measurement of position and velocity or of time and energy to more than a certain accuracy. The accuracy of each of the quantities which can be measured in a particular situation depends on the type of experiment performed. For instance, some experiments will measure the position of a particle more accurately (if it is known that the particle must pass through a small hole), while others will measure more accurately the speed. As it is impossible to simultaneously measure to an infinite accuracy all the properties of a particle in quantum physics, its future behavior cannot be completely predicted from Newton's laws of motion, which are described in chapter 2 of this book. Only probabilities can be given for what will happen in the future.

In fact, a more detailed examination of the situation raises a considerable number of other problems. Quantum theory is needed to predict what can be observed in a laboratory, that is, it describes interactions between the particles it studies, which have an effect on what happens in the world directly perceived by human beings. The relation between the world of quantum physics and that which is directly perceivable is, however, not easy to understand. On the quantum scale all possibilities of the future behavior following interactions in a system really exist; only one possibility with its associated probability of occurring will be seen in the laboratory. This is clearly seen in the famous example of "Schrödinger's cat". A cat is placed in a box in which there is a capsule containing a highly poisonous gas like hydrogen cyanide. A small hammer can break the capsule when an atom of a radioactive substance in or near the box "decays",that is, it is transformed into the atom of another chemical element, therefore emitting a particle. The particle emitted can be detected by a Geiger counter, which automatically makes the hammer strike the capsule, which then breaks. As a result of this, the cat will die almost immediately. The decay of a radioactive atom is a quantum phenomenon, and the time of it cannot be exactly predicted. At any given time, both the radioactive atom before decay and the decayed atom should exist simultaneously according to quantum theory; therefore that the cat is both living and dead simultaneously should also exist! It is because all except one of the possibilities of quantum theory appear to be eliminated in the human world, that one speaks of the "collapse" of the "wave function" (the wave function being the mathematical description of the waves). The necessity of assuming such an occurrence, which at least at first sight appears to be completely outside quantum theory, puzzled physicists for a long time. In some ways it appeared to be quite illogical.

Einstein could not accept what quantum theory had become, including its interpretation in terms of probabilities, so in spite of the fact that he was one of the "fathers" of this theory, he became opposed to its further development. He thought that real "hidden variables" were behind the probabilities and that they were the cause of the phenomena of quantum mechanics. A consequence of Einstein's opposition was that physicists were told in a scientific paper by Einstein, Podalsky and Rosen in 1935 about what appeared to be a further paradox related to wave function collapse. The paradox is now discussed in terms of what happens when "spin" is measured, that is, something corresponding to the rotation of a particle. More precisely, the spin is called the "angular momentum" of the particle. In classical physics the measured value of angular momentum depends on the direction with respect to which it is measured. In quantum theory the value of an electron, for example, can only be plus or minus half a certain physical constant in whatever direction it is measured. If two particles moving away from each other are produced with spins in opposite directions, having a total spin of zero, the measurement of the spin of one particle in a certain direction will, according to quantum theory, have an immediate effect on what spin can be measured for the other in another direction. Such a prediction contradicts what is expected from classical physics. The two particles can be far apart when the measurement is made; this measurement would appear to have an immediate effect in another place. In this way there is at least a contradiction of the spirit of special relativity, though not with special relativity itself, which does not allow bodies to be accelerated beyond the speed of light. Indeed the basic idea, in which people believe implicitly, that the events of physics are localized in separate places in space and cannot be in two places at once, seems to be in disagreement with quantum theory. Thus quantum theory violates what is called the Bell inequality, which is valid for objects of the everyday world. There is however no mathematical contradiction and the reality of this sort of surprising effect was experimentally confirmed by the work of Alain Aspect, using what are called "photons", that is, the particles associated with electromagnetic radiation, instead of charged particles.

It would therefore seem, at least at first sight, that not only has the unpredictable entered physics, but that in addition the act of measurement itself by a physicist has an effect on a real physical situation. Moreover, the normal laws of space and time of the everyday world inhabited by humans are also violated. It has become very difficult to think that the phenomena of quantum physics could be due to hidden variables localized in separate regions of space. If such hidden variables exist, as some physicists believe, they would appear to be almost certainly not localized. (We should note though, that the interpretation of the experiments showing violation of the Bell inequality is not completely watertight.) There have been many debates about the philosophical implications of the quantum theory. Bohr's "Copenhagen interpretation" tried to minimize the problems, by saying that the theory only described what happens in different experimental situations, in each of which different observations can be made. It was therefore senseless to speculate about what cannot be observed and measured. The wave and particle descriptions needed to account for the different observations made during various experiments were, according to this interpretation, complementary.

It is frequently claimed (though more often by non-physicists than by physicists, a notable exception among physicists being Eugene Wigner), that it is the conscious human observer who causes the wave function to collapse. In this way the observer, after having been eliminated as much as possible, as described in chapter 2 of this book, is again supposed to play an important role in physics. Though I shall describe in the next chapter how we can understand at least certain aspects of quantum physics by the presence of beings with a certain form of consciousness, it still seems to me rather unlikely that the human experimenter can directly produce wave function collapse. The result of an experiment can be recorded by a photograph, which is looked at much later by a physicist. Similarly, an experiment can be performed by a robot. It does not appear reasonable to say that wave function collapse occurs only when one human being, who happens to be the physicist responsible for making an experiment, is informed about the result of the experiment. What happens to Schrödinger's cat when it is not observed? Does a human being need to look at it, to see whether or not it has died? Alternatively, one might think that the cat can also collapse the wave function, but then what would be the simplest living organism able to do this? Alternatively, it has been suggested that wave function collapse occurs as a result of the agreement of all possible observers, but it is, to say the least, hard to make such an idea precise. One might even suppose that an "ultimate observer" or God produces wave function collapse, who would then be presumably outside the physics studied by almost all physicists. Indeed most would very vigorously oppose such an idea. There have in fact been claims that certain experiments show the influence of the human observer on quantum events. In particular, experiments at Princeton University by R.G. Jahn and his collaborators have been cited. These workers have even claimed an observer effect on a previous event, that is, the decay of a radioactive substance recorded by a computer! Much older (1969) experiments led to the claim that human beings could have prior knowledge of the time of decay of a radioactive atom by a sort of extrasensory perception. These results have not been, as far as I am aware, confirmed by other experimental groups. Even if true, their interpretation might be more complicated than being due to a form of wave function collapse which is directly produced by those performing such an experiment. Such an interpretation is, as we have seen, hard to conceive.

The world of modern physics has often been compared to the descriptions of the nature of the world given by mystics and in particular by eastern philosophies and religions. Bohr, for example, was well aware of a similarity between his conception of wave particle complementarity and certain aspects of Chinese thought. The parallelism of the approach of physics and of mystics is the thesis of a famous book "The Tao of Physics" by Fritjof Capra (Wildwood House 1975, Fontana 1976). Following the Copenhagen interpretation, he describes how both approaches emphasize the basic unity of the world, which is a unity of the divine or, to use Hindu terminology, of Brahman, who is in and is everything. In the Chinese tradition the unity, understood differently, is that of the Tao, which as the way or process of the universe has a dynamic quality. Mahayana Buddhism emphasizes that all things contain everything else. All is interconnected according to such conceptions; we have seen a form of interconnectedness with separation in space being overcome in our discussion of the Einstein, Podalsky and Rosen paradox. Capra also describes the paradoxes or "koans" of Zen Buddhism as being similar to the paradoxes of physics. However, the question arises as to what extent such similarities are real and to what extent they are only analogies. Moreover, at the end of his book Capra himself states that both physics and eastern mystical teachings are needed and that one cannot replace the other when we wish to describe the world.

Another approach is suggested by the definition of the wavelength of a particle. It is, as we have seen, proportional to the mass of the particle. The corresponding wavelength for a massive body of pre-quantum physics would be much smaller and it has been supposed that the paradoxical effects of quantum physics disappear when the wavelength is below what is called the "Planck length". (The corresponding minimum mass for a body moving near the speed of light is as large as about 2 hundred thousandths of a gram.) The Planck length is a theoretical length below which the effects of gravitation become more important than quantum effects; for this and for smaller lengths space should be completely different from what is known till now in physics. The wavelength of a whole cat will be far below this limit. However, this is not so for small parts of its body, which are much larger than atoms. In the same way, quantum effects could be expected even for specks of dust. Let us note however, that Penrose in the already quoted book "Shadows of the Mind", suggests a more reasonable boundary at much smaller scales of length between the world of quantum physics and that of the everyday world.

A somewhat irrational, completely materialistic way of understanding quantum theory has become quite popular, especially amongst physicists. This is the "Many Worlds" interpretation proposed by H. Everett in 1957, according to which the wave function does not really collapse when a real irreversible quantum event occurs, but rather the universe is split into several universes, which cannot communicate with each other afterwards. Such an irreversible event is defined as being a "measurement", an event which leaves an indication of having occurred at future times. If the "measurement" is the same as what is called a measurement in normal life, like one performed by physicists in a laboratory experiment, each of the different results of the measurement which are possible will be found in a separate universe. In general, each possibility in the evolution of any physical system is realized in a particular universe. The development of the sum of all these universes is completely predictable, although this "predictability" is of no use to an observer living in one of the universes. The paradox of Einstein, Podalsky and Rosen may also be overcome; there is no "action at a distance", as the properties of quantum systems at different points of space in each universe following a splitting must be consistent with each other. It was the Many Worlds interpretation of quantum physics which was referred to in chapter 2 in connection with the anthropic principle: materialists can escape the consequences of this principle if intelligent beings like humans only exist in a small proportion of the separate universes which are created according to this interpretation. Let us note that human beings have clearly no free will according to such an interpretation; all possible actions of human beings will be made in all the different universes in which humans exist. Indeed almost identical, but not quite identical copies of a reader of this book, indeed of all human beings in this universe, would exist in many different universes! We can also note that the Many Worlds interpretation may have become popular among physicists because something more like pre-quantum physics can be valid in each of the universes. In fact, the Many Worlds interpretation could possibly have been inspired by science fiction stories involving "parallel worlds". It appears to me to be a sort of science fiction way of looking at quantum physics.

An interesting way of understanding the meaning of quantum theory has been proposed by Laurent Nottale, who works at the Meudon Observatory in France. In his theory of "scale relativity" he supposes that space has basically a fractal geometry. (We discussed what fractal geometry is in the section of this chapter on chaos.) Nottale proposes that such a geometry is also necessary to describe what happens in quantum physics. In addition, he applies the idea of relativity to lengths, so that no scale of length is to be preferred to any other, in the same way as is mentioned in second section of this chapter, that no state of motion is to be preferred to any other in Einstein's special theory of relativity. The Planck length plays the same role as the speed of light in Einstein's theory. Nottale is surprisingly successful in reproducing the results of quantum theory. His theory is still far from being generally accepted, but at least shows how a more dynamic conception of space can help to overcome many problems. What is particularly interesting is that he relates quantum theory to the theory of chaos. Indeed he has also applied Schr�dinger's mathematical formulation of "wave mechanics" (mentioned in the last paragraph of section 4 of this chapter) to describe the chaotic motions of the planets. I know of no non-technical presentation of Nottale's theory in English; there is one in French which only appeared on page 34 of the September 1995 issue of "Pour la Science" (the French edition of "Scientific American").

Other interpretations of quantum theory as well as attempts to "improve" on it, have also been given. For instance it has been suggested that the wave function of any particle will spontaneously collapse after a sufficiently very long time. A massive object contains many particles, so at least one will suffer wave function collapse quite often. This should provoke the collapse of the others because of the fact that all the waves connected with the particles interact with each other according to quantum theory.

Wave function collapse is now understood by a large number of physicists as being due to the interaction between a system described by quantum physics as having both particle and wavelike properties and the extremely numerous particles associated with a very large number of waves of the large scale world. The latter clearly includes any laboratory apparatus used to carry out a measurement. In the description of the world on the human scale, we do not consider the quantum behavior of every particle associated with waves of which it is made; all we wish to know about it can be described in much less detail. The rest, which is not needed in the description, is called by physicists the "environment". It is the interaction of the quantum world with this "environment", associated with the large scale world, that is thought to cause wave function collapse. For this reason we do not perceive the quantum behavior of every particle inside Schrödinger's cat; the presence of such an "environment" (the body of the cat) is thought to cause the cat to be seen to be either dead or alive, even though it may be poisoned as a result of a quantum phenomenon. This way of producing wave function collapse is called "decoherence"; the idea comes from the work of several physicists, including that of W. Zurek (Readers with knowledge of physics can read a review by Zurek on page 36 of the October 1991 issue of "Physics Today"). It may be noted in this connection that the presence of chaotic phenomena such as those discussed in section 3 of this chapter can also lead to decoherence. Decoherence may be thought of as a way of making real for an observer in the large scale world only one possible history of the universe which has a probability that it will occur. Each possible history must in addition obey the laws of logic of this large scale world. The existence of the phenomenon of decoherence is now supported by laboratory experiments (see article by S. Haroche on page 36 of the July 1998 issue of "Physics Today").

Though all interpretations of quantum physics have not been mentioned in this section, it might appear, at first sight, that everything can be explained by blind unconscious processes of matter, unless claims concerning experiments which could suggest the action of the human experimenter are confirmed. In fact, physicists view matter, energy, space and time in a very different way than in the nineteenth century. These concepts have become very abstract and mathematical. Physicists are still, however, usually materialists; they continue to base their reasoning on the space and the space-like aspects of time. A somewhat different way of seeing a form of soul behind modern physics can nevertheless be proposed, as we shall see in the next chapter.

Present-day physics says other things about the nature of matter. Before leaving this description of contemporary physics, I shall mention a few of them. They are mainly those needed in discussions later in this book.

Firstly, let us consider why, according to physics, different kinds of atoms keep their various structures and indeed why do they not collapse; that is, why don't the negatively charged electrons attracted by the positively charged nucleus of an atom first come very close to it, before falling in? If that happened, matter as we know it should then also collapse. Physics gives two reasons for the stability of matter. Firstly, the wave nature of particles is invoked; the wave structures of wave mechanics described mathematically by Schrödinger's wave mechanics, do not collapse. This can be explained in an approximate though not quite rigorous way using the Heisenberg indeterminacy principle, mentioned in the last section. If we think about an atom of hydrogen, which is understood to have only one electron, the position of the electron relative to the small nucleus would need to become extremely precise when it fell into the nucleus. Now, by the first form of the Heisenberg principle given in the last section, which relates the maximum accuracy to which its position can be defined to the corresponding maximum accuracy for its velocity, the position could only be very precise if the exact value of the velocity were not well defined. In this way the range of possible velocities of the electron can be large enough in such a situation to enable it to have a large enough velocity to escape from the strong electrical attraction of the nucleus!

There is another reason, called the Pauli exclusion principle, to explain why atoms retain their different structures. Only two electrons can have the same wave structure, for which the "quantum state" will be almost the same. This means that when an atom has many electrons, each pair of electrons will have another wave structure. To be more rigorous and precise, the spin of an electron section needs to be taken into account. The spin can, as mentioned previously, only be equal to plus or minus a half of a basic constant of spin. The two electrons having the same wave structure will have opposite spins and the quantum state will be the same except for the spin. Let us recall that only certain stable lasting wave structures are possible according to wave mechanics. In this way the different properties of atoms with differing numbers of electrons are explained. In any case, it is clear that all electrons cannot acquire at the same time the same wave structure as close as possible to the nucleus.

Ideas about which particles are fundamental have changed in the last decades. As mentioned in section 4 of this chapter, the nucleus of an atom is considered to contain different particles called protons and neutrons. These particles are not now thought to be fundamental; each of them is believed to contain three fundamental particles called "quarks". Many other kinds of particles, such as the electrons frequently referred to in this chapter, are believed to be fundamental. Such particles are divided into two categories. Those of the first category called "fermions" (named after the Italian physicist Enrico Fermi) obey the Pauli exclusion principle; no two fermions can be in the same quantum state. "Bosons" of the other category (named after the Indian physicist S.N. Bose) do not obey such a principle. The spins of the two sorts of particles are not the same; bosons have spins which are whole number multiples of the basic constant of spin, while fermions have spins which are whole number multiples of this constant plus one half. Fermions include electrons and quarks. Evidence has been obtained by physicists of the existence of three families of fermions. The already mentioned particles called "photons", associated with electromagnetic radiation, are examples of bosons. Let it be in addition noted that each sort of particle has in this framework what is called an "antiparticle" with "opposite properties"; for example the electron with a negative electrical charge has the positively charged "positron" as antiparticle. When an electron meets a positron, both are annihilated, leading to the production of photons. On the other hand, the photon is its own antiparticle. The fact that many sorts of "fundamental" particles have been discovered appears to be somewhat embarrassing, though it is true that the different types of particles which are believed to exist can be classified in a mathematically simple way. Attempts are being made by theoretical physicists to explain all this complexity. At present physicists consider what is called "superstring" theory, to be very promising. A popular account of these things is given in "The Quark and the Jaguar. Adventures in the Simple and the Complex" by Murray Gell-mann (Little, Brown and Co. 1994).

Physicists now explain the forces of physics by the action of different sorts of fundamental particles. This is quite different from the explanations given in the nineteenth century. Let us start with electricity and magnetism, whose description was, as mentioned in section 2 of chapter 2, unified in the nineteenth century by Maxwell's electromagnetic theory. Light was explained as consisting of electromagnetic waves, visible to the human eye. Light was explained as being due to electricity and magnetism. Modern theory reverses this explanation. Photons, that is the particles associated with light and other sorts of electromagnetic waves, are used to explain electricity and magnetism. This explanation also involves the second version of the Heisenberg indeterminacy principle given in section 5 of this chapter, which permits the spontaneous creation of photons, containing energy, for very short times, before they disappear again. When such a particle only exists for a very short time, the uncertainty in the time during which it can exist is very small, but the uncertainty in its energy is then very large. Such a spontaneously produced particle can therefore have a large undetectable energy before it disappears again. If on the contrary such a particle exists for a very long time, the uncertainty in its energy is very small. Therefore only a particle with a small amount of energy can be spontaneously created in the second case. A particle of this sort, which is created in such a spontaneous way and which is not directly detectable before it disappears, is called "virtual". The present quantum explanation of electricity and magnetism then involves the exchange of virtual photons between other particles, which are electrically charged.

The force which binds quarks inside protons and neutrons is called the "strong interaction". It is an indirect effect of this force which is invoked to explain the already mentioned "nuclear force", which keeps the positively charged protons and the electrically neutral neutrons in the nucleus of an atom. Physicists explain the strong interaction by the existence of several kinds of another type of "fundamental" particle, the "gluon"; virtual gluons are considered to be exchanged between quarks, in the same way that virtual photons are supposed to be exchanged between electric charges. This exchange appears to be more complicated than in the case of electricity and magnetism; while only two sorts of electric charges exist (positive and negative), three sorts of the corresponding "charge" exist for the strong interaction.

Another force which influences radioactivity is called the "weak interaction". This is thought to involve the exchange of still other kinds of fundamental particles. The unification of the theory of the weak interaction with that of electromagnetism is a great triumph of recent theoretical physics. The theory of the strong interaction is moreover also mathematically close to that of electromagnetism and the weak interaction. This suggests the possibility of a grand unification of both.

Gravitation is yet another force, which is in principle explainable in a similar way by the exchange of "gravitons". In fact, it is not easy to integrate gravitation in this scheme, though the already mentioned "superstring theory" would appear to be capable of this.

In these explanations of the fundamental forces of physics, the virtual particles which are exchanged are bosons. In this way we can see a polarity according to present-day physics. Fermions which cannot occupy the same quantum state produce the structure of matter, while bosons which can occupy the same quantum state, produce the forces of physics.

The existence of virtual particles leads to very complicated processes. A virtual particle can in its turn give birth to another virtual particle. For instance, under certain conditions a virtual photon can create a virtual electron and a virtual positron (the opposite process to their annihilation). The virtual electron and virtual positron can in their turn create virtual photons; such a succession of processes has no end. Each sort of detectable particle is, according to these ideas, surrounded by a cloud of virtual particles. This "reproduction" of virtual particles may remind the reader of the proliferation of "life" in the normal world of human experience.

Theoretical physicists would like to formulate a "theory of everything" using the concepts of the last three sections of this chapter. This ultimate dream of materialists is clearly not possible. Even if no reference is made to any sort of spiritual teaching, physics only based on space and the space-like aspects of time cannot explain the second and third worlds of Karl Popper and Roger Penrose, described in chapter 1. However, as we shall see, there are still important lessons to be drawn from twentieth century physics. These include, especially, the fundamental roles played by the Heisenberg indeterminacy and Pauli exclusion principles in what modern physics believes to be the basis of matter.

I shall now come to what I once heard described as the most amazing discovery of the twentieth century. The field of Mathematics is usually held up as an example of what is certain, of what can be rigorously proved and where it is possible to banish doubt. This view of mathematics was shaken at about the same time as the collapse of the idea of absolute predictability in physics. The consequences of what happened in mathematics are perhaps even more far-reaching. A popular description of the how the previous development of mathematics led to this "disaster" is given by Morris Kline in "Mathematics: the Loss of Certainty" (Oxford University Press 1980).

In the same way that nineteenth century physicists wished to predict everything from the laws of physics, mathematicians wished to be able deduce all possible results in mathematics from a few fundamental principles. A good example of how this can be done is elementary geometry, which was developed by the ancient Greeks. Euclid proposed a number of "axioms", that is, fundamental principles on the basis of which all kinds of geometrical results called "theorems" can be proven. For instance, it is possible to prove in such a way the famous Pythagorean theorem of for a right-angled triangle, The square of the length of the hypotenuse equals the sum of the squares of the lengths of the other two sides (fig 3.5). One of Euclid's axioms about where two straight lines, crossed by another line, will intersect has, in fact, an uncertain validity; if it is dropped, other "non-Euclidean" geometries, discovered in the nineteenth century, become possible.

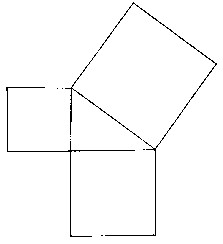
Fig. 3.5 - Pythagoras' Theorem. The square of the longest side of a right-angled triangle is equal to the sum of the squares of the other two sides.

By the nineteenth century many concepts had entered mathematics which could not be logically justified; it was then that mathematicians started seeking a logical basis to the whole of mathematics. A fair amount of progress was made at that time. In the early years of the twentieth century, different schools existed with different opinions about the foundations of mathematics.

One school included G. Frege, Bertrand Russel and Alfred North Whitehead. They tried to base mathematics on the laws of logic. Numbers are the basis of mathematics, so in order to possess secure foundations, it was necessary to find a logical basis for the concept of what a number is. However, the attempt to base mathematics on logic led to a number of difficulties; in particular certain axioms of doubtful validity were needed. In the end, Bertrand Russel himself admitted the failure of the attempt.

Another school, opposing the attempt to base mathematics on logic and led by L.E.J. Brouwer, a Dutch mathematics professor, was called "intuitionist". Brouwer asserted that mathematics was an activity of the human mind which had no real existence outside it. The mind is able to have direct intuitions of mathematical principles. Intuition then determined the soundness and acceptability of ideas, which were neither determined by experience nor by logic. Acceptable logic is to be based on mathematical intuition. The idea of deducing mathematics from basic axioms was rejected. The result of this type of approach in the end was, as might be expected, that many mathematical methods and results could not be accepted.

The leader of a third "formalist" school was the German mathematician David Hilbert. He disagreed with the idea of basing the concept of whole numbers on logic; for him whole numbers were already implicitly present in logic from the beginning. He was also alarmed by the intuitonist approach, which rejected large parts of mathematics. Hilbert wished to found mathematics on basic axioms which needed to be consistent with each other. These axioms involved both mathematics and logic. He proposed to use a special logic to show that there were no inconsistencies in mathematics.

In any case, two basic problems concerning the foundations of mathematics remained in 1930. The first was to prove that it was impossible to obtain contradictory results in mathematics, that is, that mathematics was consistent with itself. The other problem was how to establish a complete set of axioms for any branch of mathematics from which everything could be derived. In 1931 the Austrian mathematician Kurt Gödel showed that it is impossible to resolve these problems. It is not possible to prove that there are no contradictions in any mathematical system which includes the arithmetic of whole numbers! In addition, any theory of whole numbers is incomplete; that is, that if one has a finite number of axioms there are mathematical statements which can be neither proved nor disproved! It was in this way that a sort of indeterminacy entered mathematics, as it had entered physics.

In 1936, Alonzo Church showed that in general there is no way of deciding in advance whether a mathematical statement is provable or not. As a result, mathematicians cannot have standard procedures for proving things, even though they may be provable. This can also be understood as stating that they have to work to prove things; they are not in danger of becoming unemployed.

A good example of such problems is Fermat's famous last theorem, stated by the seventeenth century French mathematician Pierre de Fermat. It concerns what happens when three whole numbers are raised to the power n; that is, are multiplied by themselves n -1 times. The question is when do three different whole numbers A, B and C exist, which satisfy the following expression:

Aⁿ + Bⁿ = Cⁿ

This is clearly possible when n equals 1, so they are not multiplied by themselves; all whole numbers except zero, one and two can be set equal to sums of two other different positive whole numbers. When n equals 2 this is still possible in certain cases, such as 3 times 3 plus 4 times 4 equals 5 times 5, or:

3² + 4² = 5²

another example is:

5² +12² = 13²

Fermat's last theorem is very simple; it states that when n is greater than 2, no whole numbers exist satisfying such a relationship, unless either A, B or C is zero. Though Fermat claimed to have found a proof, a rigorous proof was in fact only found with difficulty by the Princeton University mathematician Andrew Wiles in 1994. At one time the theorem was suspected of being unprovable.

The results of Gödel and Church indicate that no mechanical procedure can be invented to make all mathematical proofs. A result is that all such proofs cannot be made by a computer following fixed rules. The English mathematician Alan Turing, who was also one of the fathers of the theory of computers, conceived a model of an ideal computer, which is called a Turing machine. Such a machine can be considered to have solved a mathematical problem if, after starting the calculations needed to solve it, it comes to the end and stops. This type of machine can, in many situations, continue to compute without ever stopping, without it being possible to give a general rule about when this will occur. In fact if a general rule existed, a basic contradiction would occur in certain cases; it would be possible to prove for certain mathematical statements that it is impossible to prove or decide whether a particular statement is true or not! As a result the general rule cannot exist, as is explained by Penrose in "Shadows of the Mind". Such reasoning is similar to that used to prove Gödel's theorem itself. This type of difficulty arises because a mathematical statement can be about itself, that is, a process of thinking can be about itself.

Arguments of this type are used by Penrose in "The Emperor's New Mind" and "Shadows of the Mind", to show that computers, constructed according to known principles, cannot reproduce all human thinking. Such a computer can only follow well defined rules. Penrose supposes, however, that a computer working according to the rules of quantum physics might overcome this problem. He suggests that the human brain functions as a machine of this type. In "Shadows of the Mind" he proposes a rather speculative model involving the action of quantum physics in the working of the brain's nerve cells. However, he does not prove that human thinking can be reproduced in such a way.

The first conclusion which can be drawn is that although many aspects of thinking can be imitated by mechanical processes, it is extremely difficult to imitate all aspects of thinking in this way. If the brain is only a predictable mechanical system, it would appear to be incapable of being completely responsible for producing all of what is involved in thinking. We may then suppose that the brain is not able to think about thinking itself. It appears to me that the only possible way one might try to escape from such a conclusion would be to invoke the probably unpredictable chaotic nature of the brain, which as a result of minute perturbations to it could then arrive at thoughts, which do not directly follow from previous thoughts... However, it would appear to most people that thinking about thinking is clearly not an irrational process!

The basic importance of thinking as an autonomous activity was emphasized on a much more fundamental level by Rudolf Steiner, particularly in his "Philosophy of Freedom", mentioned in chapter 1. He pointed out that thinking is a basic human experience and showed that man's knowledge of the world is obtained from both observations of what is perceived and thinking, each being necessary right from the beginning. Thinking is in this framework an activity directed at the perceptions of an object observed by the self of a human being, who is immediately aware of this activity. The content of thoughts and how one passes from one thought to another cannot be governed by any process involving the physics of the brain, but must be only governed by the laws of thought. This is clearly the case in any sort of scientific activity, where it is impossible to escape from thinking. In his Philosophy of Freedom, Rudolf Steiner wrote: "My observation shows me that in linking one thought to another there is nothing to guide me but the content of my thoughts. I am not guided by any material process in my brain. In a less materialistic age than our own this remark would of course be entirely superfluous". According to Rudolf Steiner, it is in the world of pure thinking and in actions inspired by this activity, that a human being can be free.

Gödel's theorem suggests even more striking conclusions about the nature of mathematics and the world of pure ideas studied by it, to be discussed in the next chapter.

© 1999 Michael Friedjung

Michael Friedjung was born in 1940 in England of Austrian refugee parents who had escaped from the Nazis. He was already deeply interested in science at eleven years of age, and uniting science and spirituality eventually became his aim. He studied astronomy, obtaining a Bsc in 1961 and his Phd in 1965. After short stays in South Africa and Canada, he went to France in 1967 on a post-doctoral fellowship and later was appointed to a permanent position at the French National Center for Scientific Research (CNRS) in 1969, where he is now Research Director. After living with the contradictions between official science and spiritual teachings, he began to see solutions to at least some of the problems, which are described in this book.

E-mail: [email protected]

Chapter 3, Part 1

Return to Home Page